مدت مطالعه: 7 دقیقه
مدت مطالعه: 7 دقیقه معمای المپیادی
آیا برای حل معماهای سخت آماده هستید؟ دوست دارید معماهایی در سطح معماهای المپیادی حل کنید و هوش خود را محک بزنید و خودتان را به چالش بکشید؟
حل معماهای المپیادی گزینه خوبی برای به چالش کشیدن خود می باشند؛ برای حل این معماها آماده اید؟
|
برای دسترسی آسان و سریع به هر بخش بر روی آن کلیک کنید:
|
معمای المپیادی تصویری |
معمای المپیادی شماره 1
قصد داریم میان دو نقطه طوری حرکت کنیم که هر کدام از اعداد 0 تا 4 دقیقا یک بار در طول مسیر ما باشد؛ حال به چند راه میتوان از نقطهی A به نقطهی B رفت به طوری که هر یک از اعداد ۰ تا ۴ دقیقاً یک بار در طول مسیر در نقطه ها دیده شوند؟
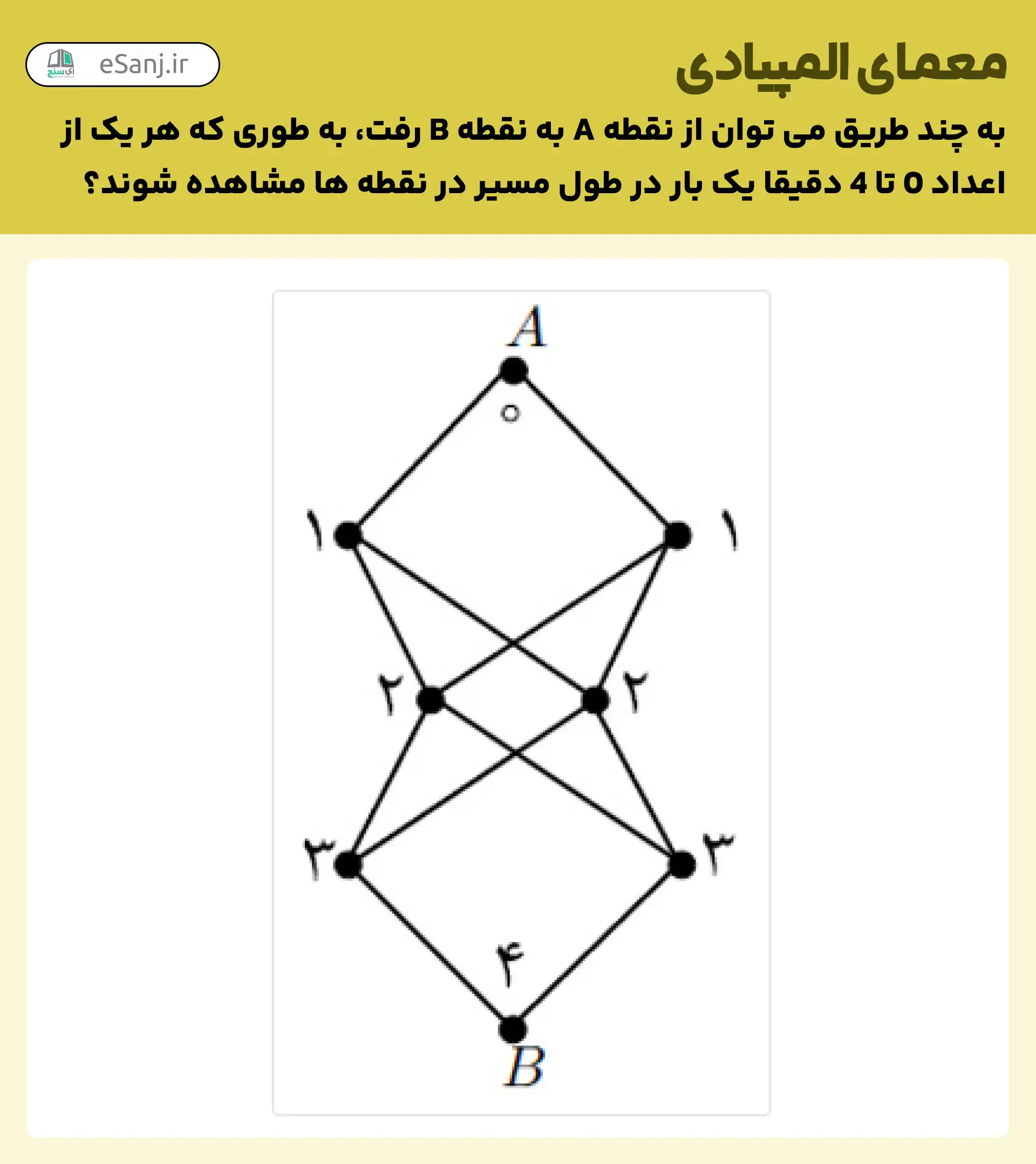
8 بار می توانیم این مسیر را طی کنیم.
معمای المپیادی شماره 2
حداکثر چند دایره از دایره شکل مقابل را می توان پر کرد، طوری که هیچ دایره پر شده ای رئوس یک مربع یا مستطیل با اضلاع افقی و عمودی نباشند؟

اگر ستونی هر سه دایرهاش پر باشد در این صورت واضح است که از هر کدام از چهار ستون دیگر فقط یکی از دایرههایشان میتواند پر باشد زیرا در غیر این صورت مربع یا مستطیل با چهار راس پر پیدا خواهد شد. دراین صورت 4×2 دایره سفید موجود خواهد بود که معلوم میشود ۷ دایرهی پر وجود دارد.
و اما اگر هیچ ستونی هر سه دایرهاش پر نباشد در این صورت یکی از ستونها (مثلا اول) که دو دایرهاش پر میباشد را در نظر میگیریم. به عنوان مثال فرض میکنیم دو سطر اول ستون اول پر باشند بدیهی است که در چهار ستون دیگر دو سطر اول و دوم تواما نباید پر باشند و همچنین از ۴ دایرهی مربوط به سطر آخر چهار ستون پایانی حداکثر ۲ دایره میتواند پر باشد. پس کل دایرههای پر 2+4+2 یعنی ۸ دایره میتواند باشد که نمونهای از آن در شکل زیر قابل مشاهده است.

معمای المپیادی شماره 3
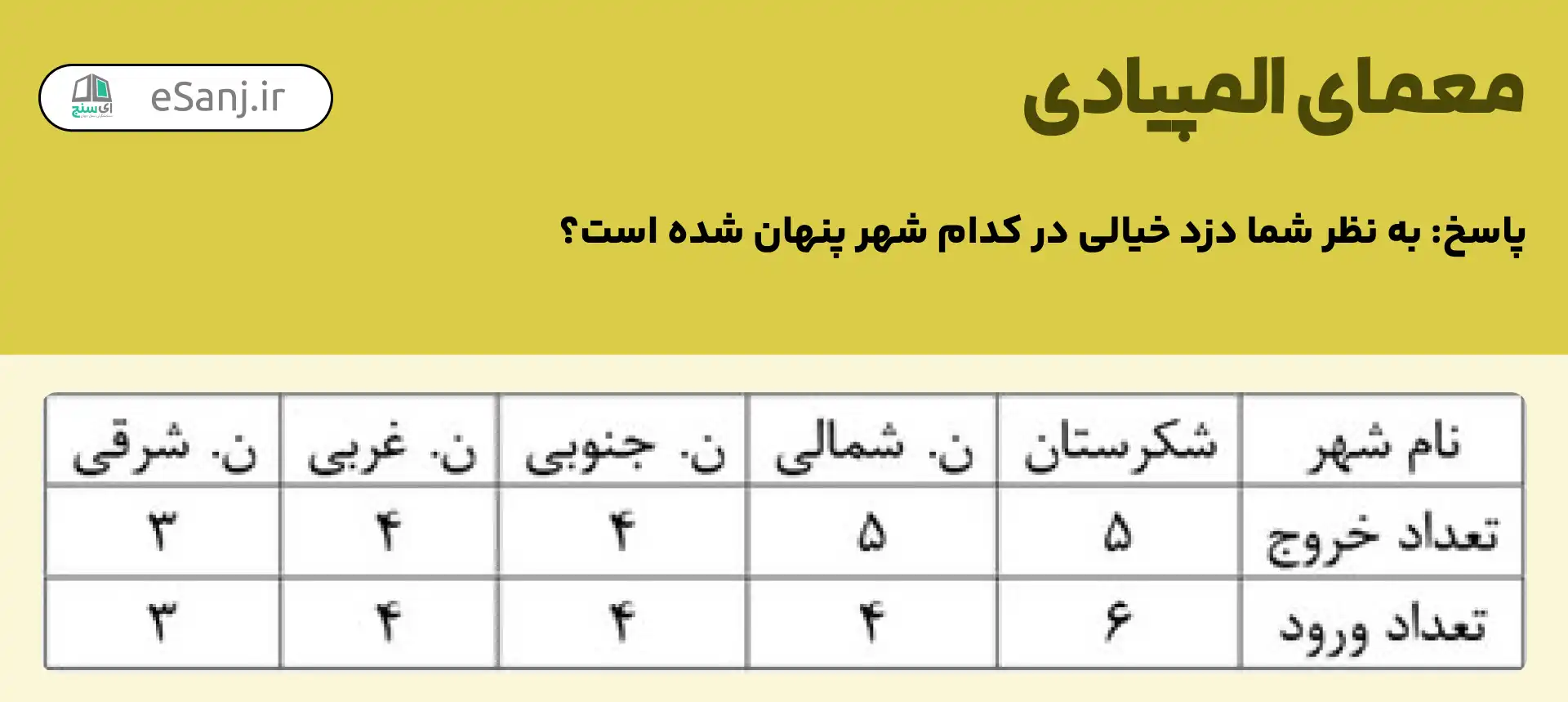
روستای خیالی دزدی در حال تعقیب دارد؛ تعداد سفرهایی که او به شهرهای شکرستان داشته است در جدول زیر آمده است؛ به نظر شما او در حال حاضر در کدام شهر پنهان شده است؟
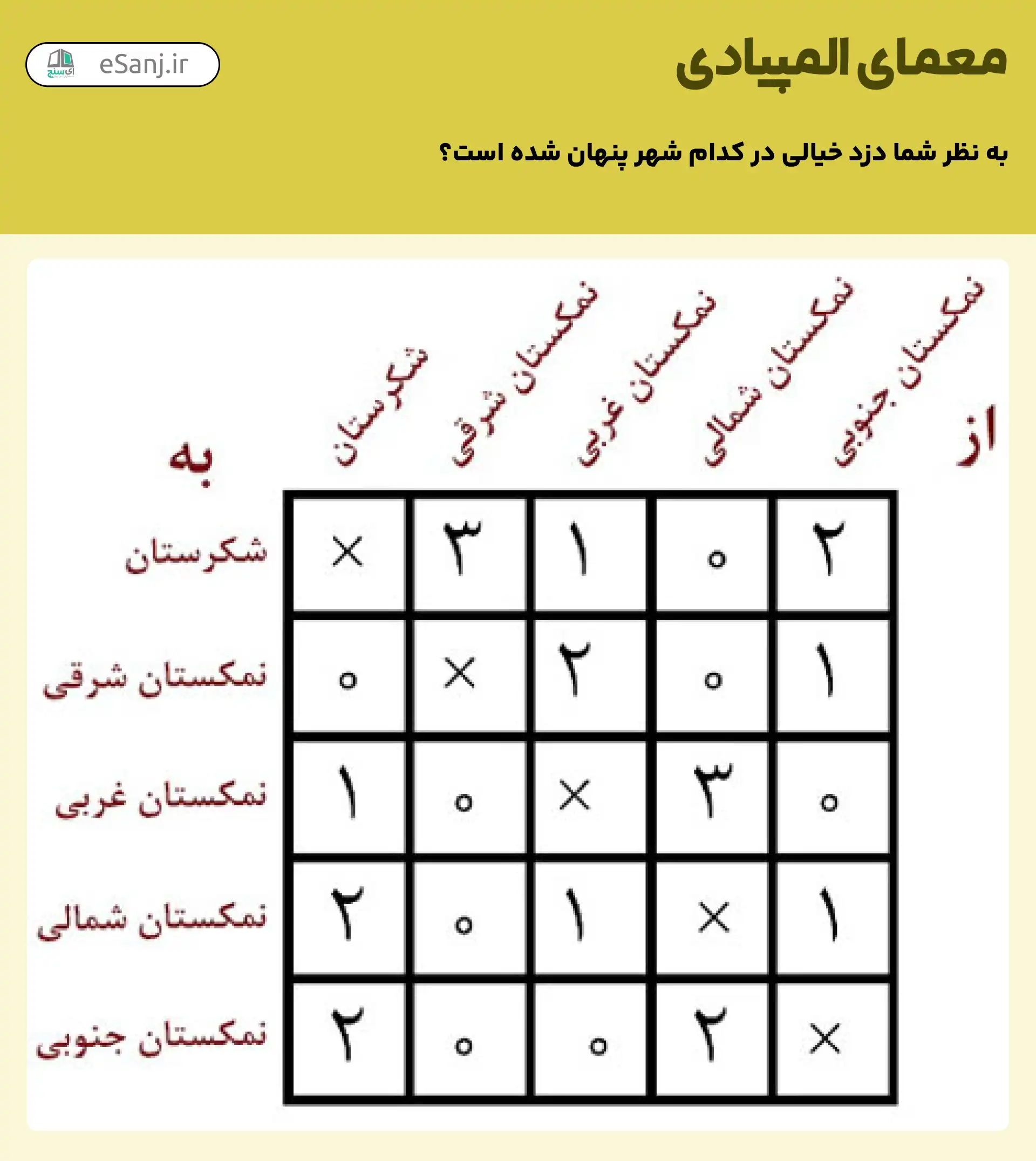
این دزد بر اساس آنچه در جدول آمده است، 5 بار از شهر شکرستان خارج شده و 6 بار به این شهر برگشته است. پس او در شهر شکرستان است.
معمای المپیادی شماره 4
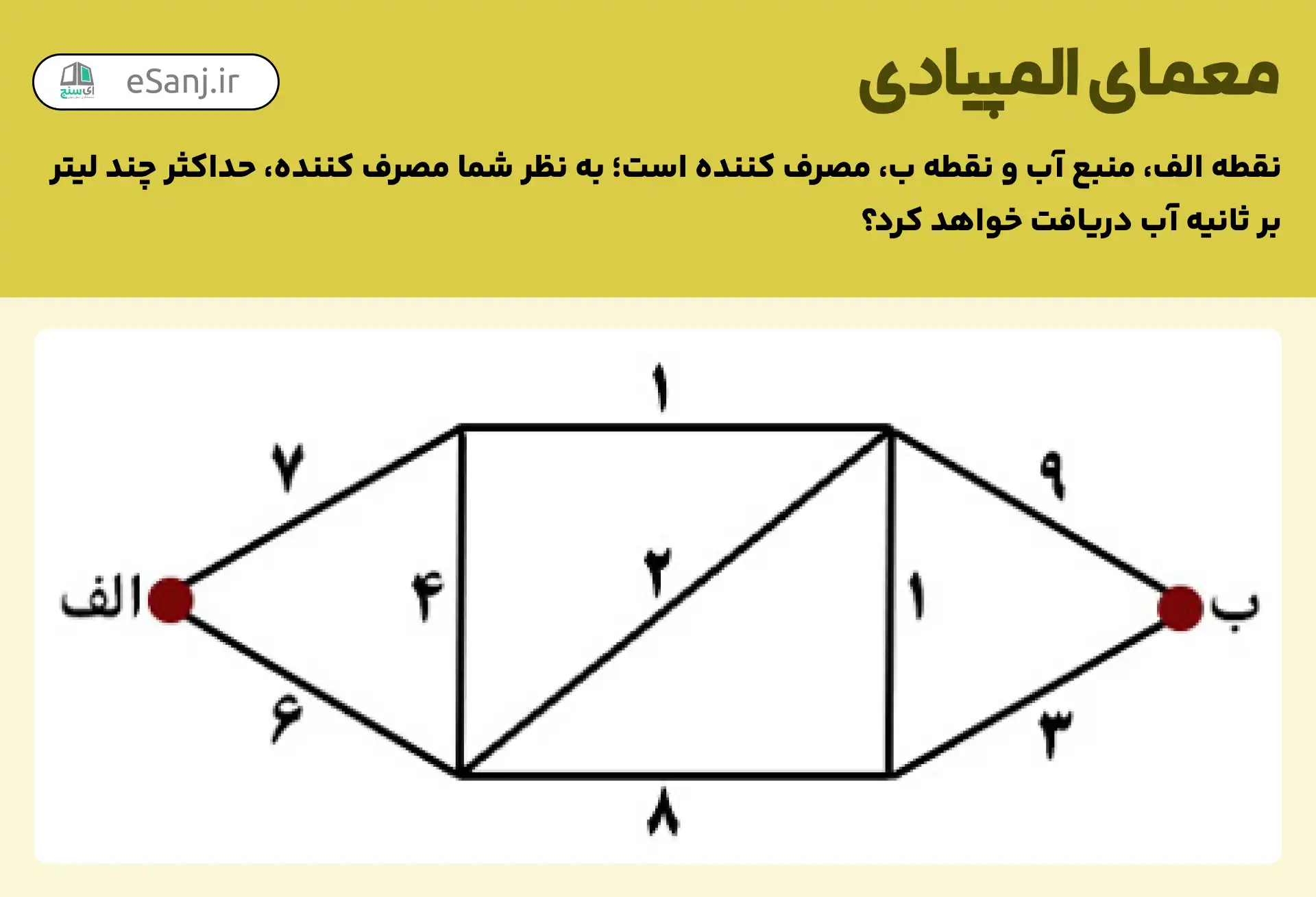
شکل زیر یک لوله آبرسانی است که ساختار مشخصی دارد و برای انتقال ظرفیت متفاوتی از آب لوله کشی شده است؛ در شکل زیر نقطه الف منبع آب و نقطه ب، مصرف کننده است. اعدادی که نوشته شده است بیانگر حداکثر ظرفیت انتقال آن لوله بر مبنای لیتر بر ثانیه می باشد.
به نظر شما از نقطه الف تا ب، حداکثر چند لیتر آب بر ثانیه به مصرف کننده خواهد رسید؟
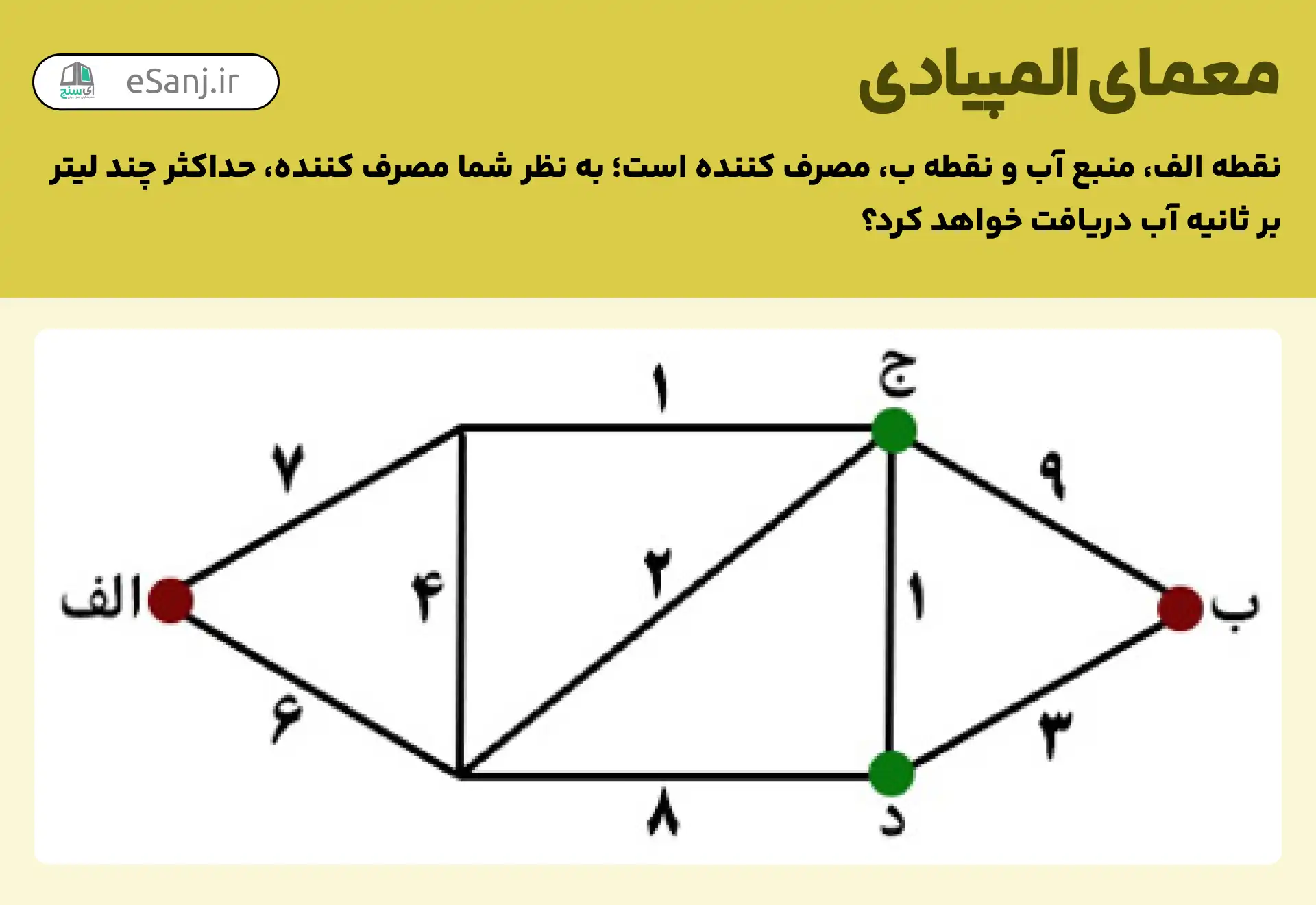
بر اساس آنچه در شکل آمده است، حداکثر ۴ لیتر آب به نقطهی ج میرسد. پس از لولهی ب-ج که ظرفیت آن ۹ لیتر است حداکثر ۴ لیتر در ثانیه آب به مصرف کننده ب سرازیر میشود.
از لولهی ب-د نیز که حداکثر ظرفیت آن ۳ لیتر است اگر ۳ لیتر در ثانیه آب به مصرفکننده ب برسد حداکثر آبی که به مصرف کننده خواهد رسید ۷ لیتر در ثانیه میباشد.
معمای المپیادی شماره 5
اگر در این کوزه با نرخ ثابت، در هر دقیقه یک لیتر آب می ریزیم؛ کدام یک از نمودارها، می تواند نشان دهنده ارتفاع آب بر حسب زمان باشد؟

ارتفاع آب در طول زمان همواره صعودی است.
شیب نمودار در هر لحظه تابعی نزولی از مساحت هر قطاع ظرف است.
پس ابتدا باید شیب زیاد باشد و به مرور زمان کم شود تا به قسمتی از خمره برسد که بیشترین مساحت را دارد و سپس دوباره شیب افزایش پیدا می کند.
پاسخ صحیح گزینه (ب) می باشد.
معمای المپیادی شماره 6
چند مثلث در این تصویر می بینید؟

۲۹ مثلث.
به ازای انتخاب هر سه نقطه، یک مثلث پدید می آید، مگر آنکه آن سه نقطه در یک امتداد باشند.
معمای المپیادی شماره 7
کارت های زیر، کارت هایی است که در یک بازی ابداعی به کار می رود؛ در این بازی قرار است هر دو کارت دقیقا یک گزینه مشابه و مشترک داشته باشند؛ اعداد این کارت ها از یک تا هفت می باشد و روی هر کارت سه عدد متمایز از میان این اعداد نوشته می شود.
قصد داریم کارت ها را به گونه ای طراحی کنیم که دو کارت متمایز دقیقا یک عدد مشترک داشته باشند؛ به نظر شما حداکثر چند کارت متفاوت خواهیم داشت؟
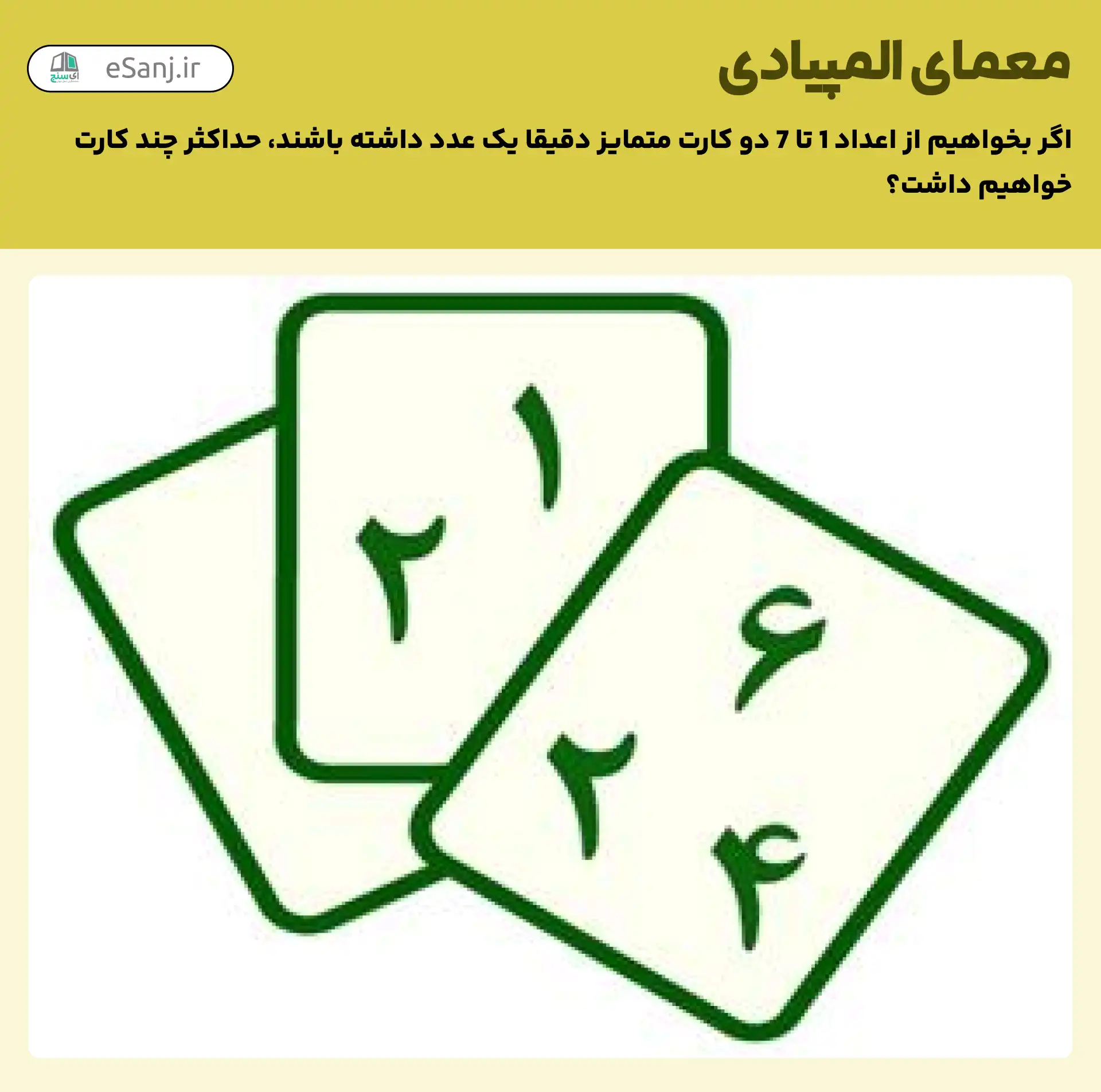
7 کارت با اعداد زیر خواهیم داشت:
مشخص است که هر عدد در حداکثر 3 کارت قابل درج است، زيرا اگر عددي مانند x در چهار کارت درج شود، تمام هشت عدد ديگر در اين چهار کارت بايد متمايز باشند که به دليل وجود تنها 7 عدد متمايز امکان پذير نيست.
در نتيجه تعداد کل کارتهاي قابل ساخت حداکثر 7/3×3 است. اين 7 کارت را ميتوان به شکل زير ساخت:
(1,2,3) ,(1,4,5) ,(1,6,7) ,(2,4,6) ,(2,5,7) ,(3,4,7) ,(3,5,6)
همانطور که در شکل بالا مشاهده می کنید، از نقطه A به نقطه B، تعدادی مسیر وجود دارد. مسیرها در جهت فلش، یک طرفه هستند. به چند طریق می توانیم مسیر یک طرفه را طی کنیم؟
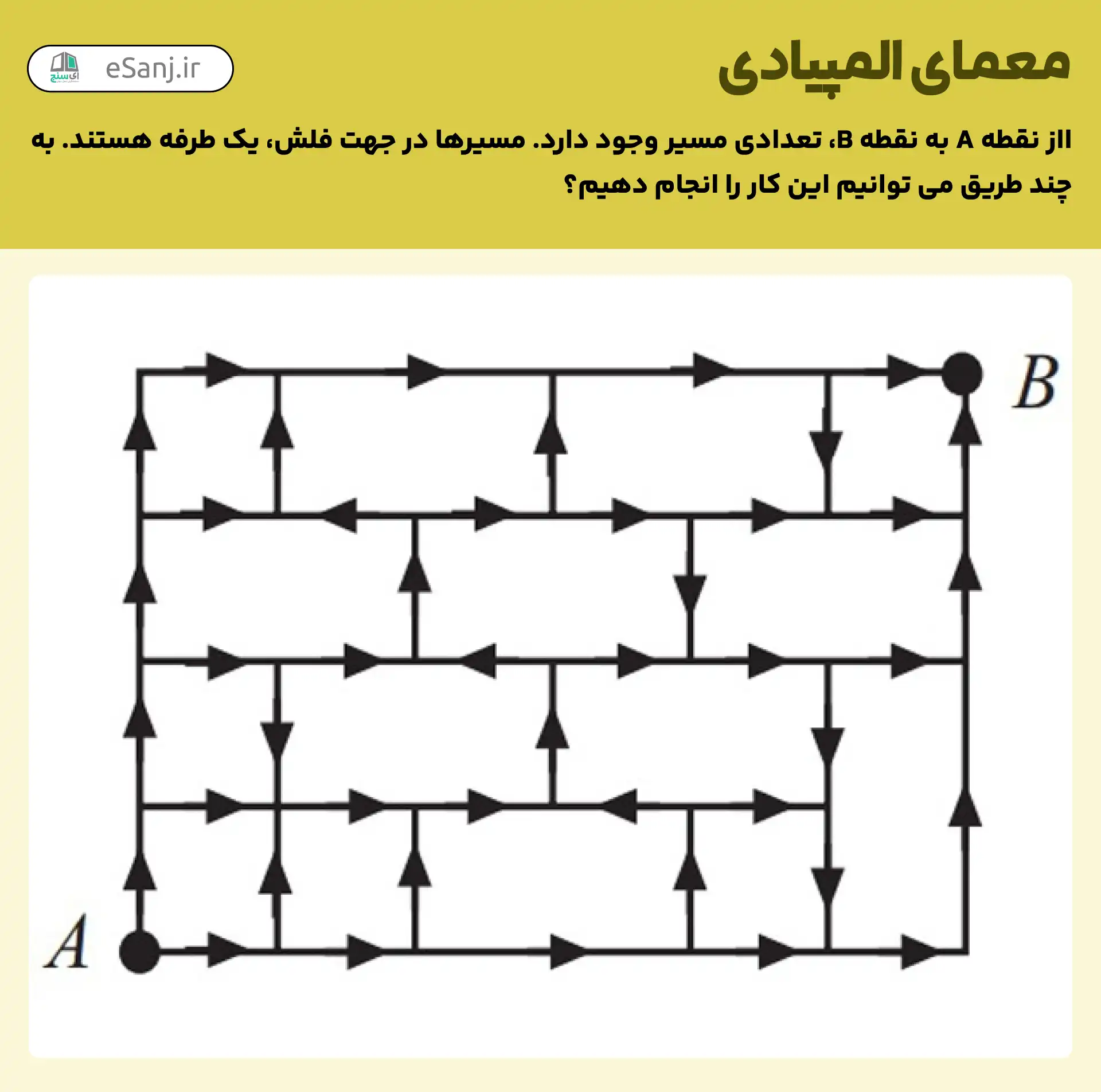
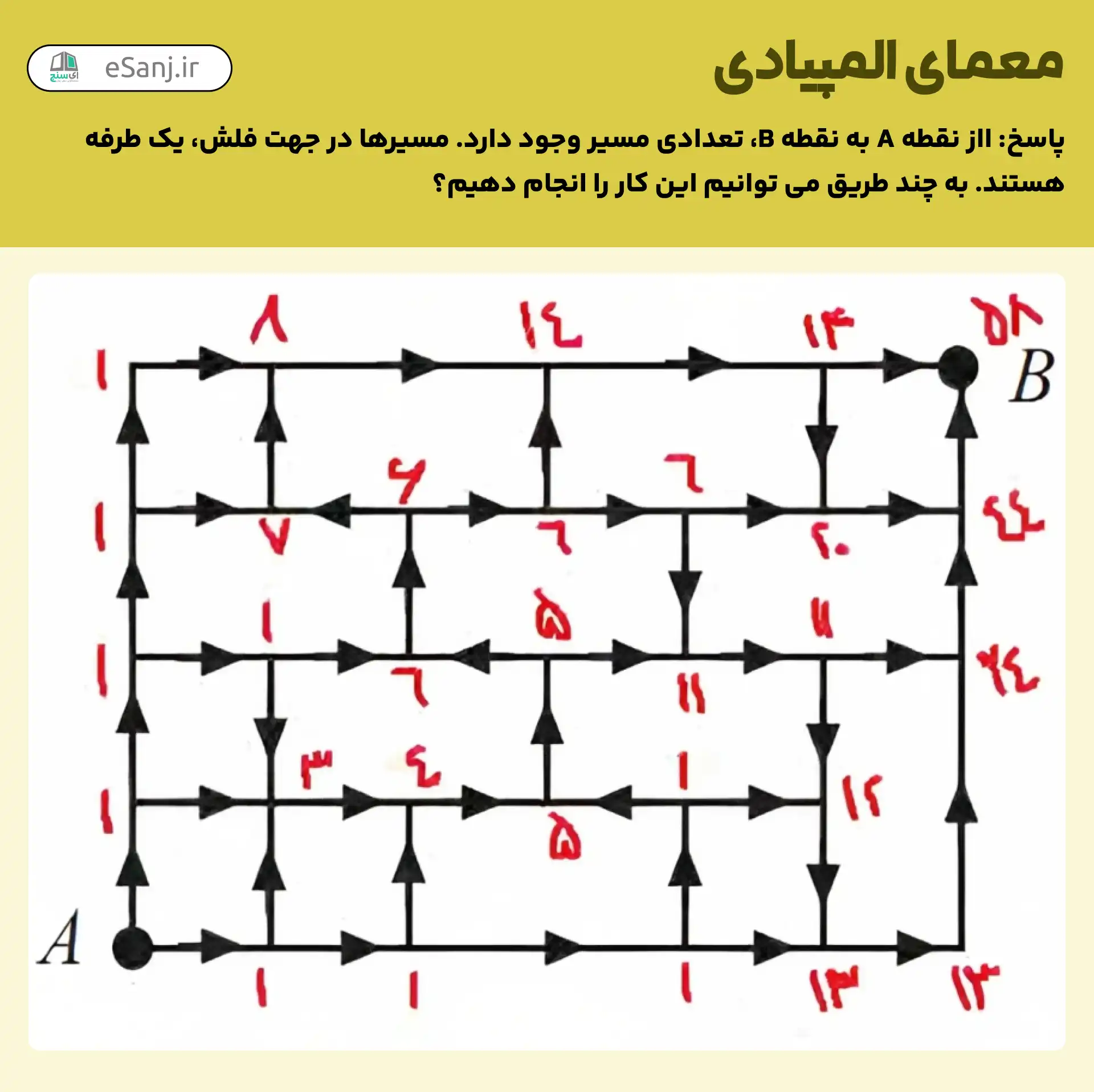
58 بار .
طبق اصل جمع تعداد راه های رسيدن به هر نقطه برابر است با جمع تعداد راه هايی که می توان به آن نقطه رسيد و بر همين اساس تعداد راه های رسيدن به هر نقطه را محاسبه می کنيم :
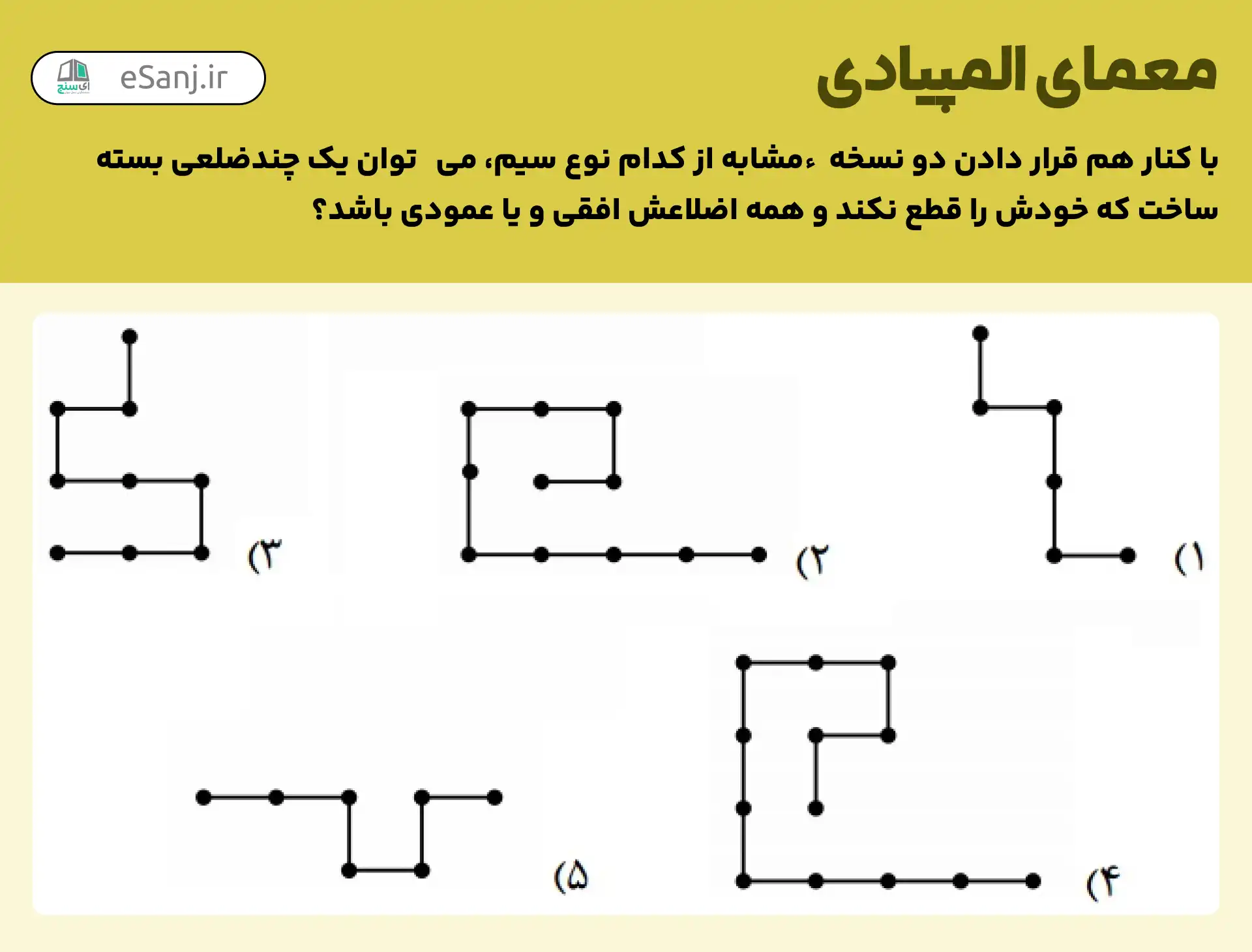
با کنار هم قرار دادن دو نسخه شبیه بهم از کدام نوع سیم می توان یک چند ضلعی بسته ساخت که خودش را قطع نکند و همه اضلاعش افقی یا عمودی باشد؟
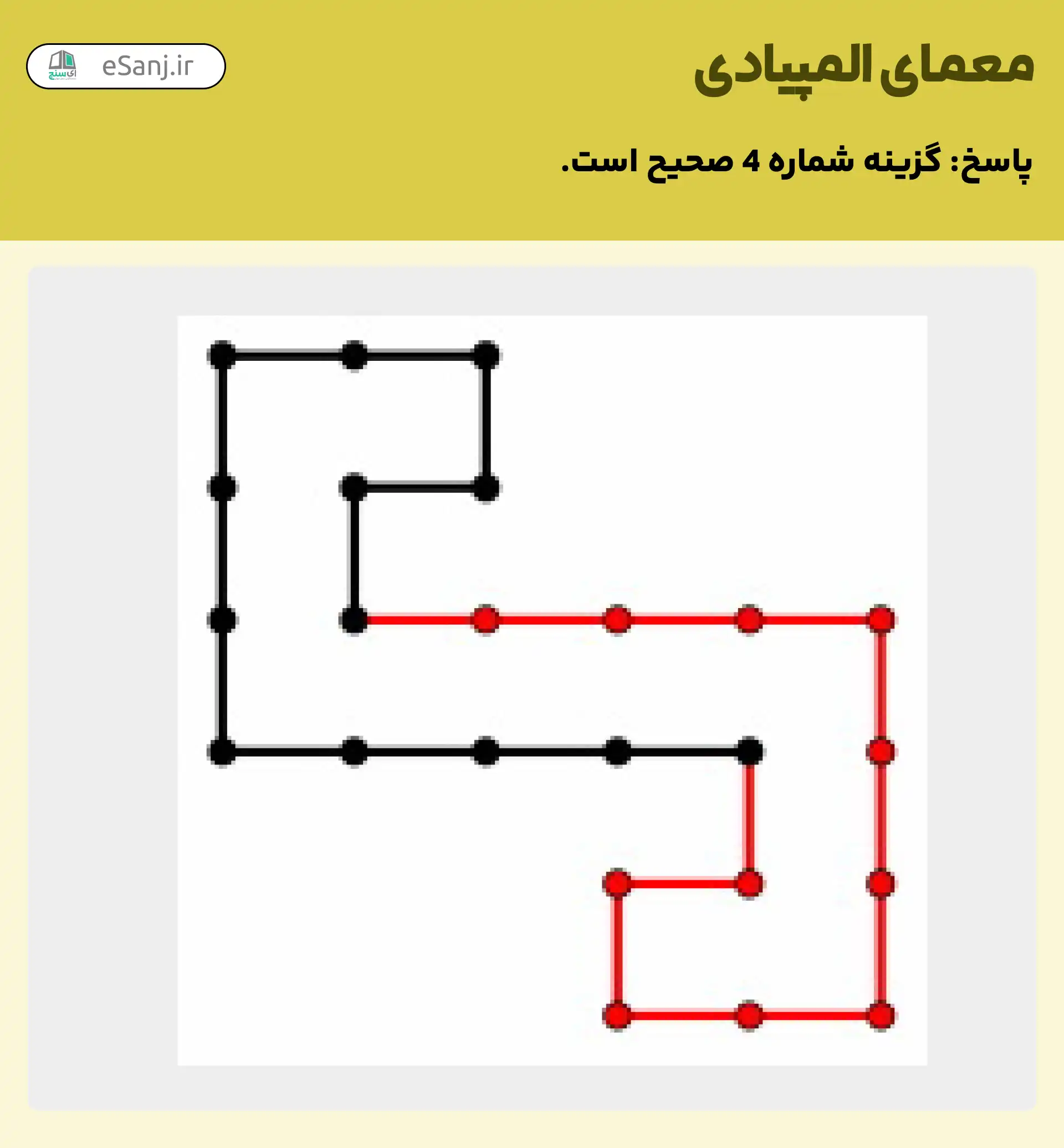
معمای المپیادی شماره 10
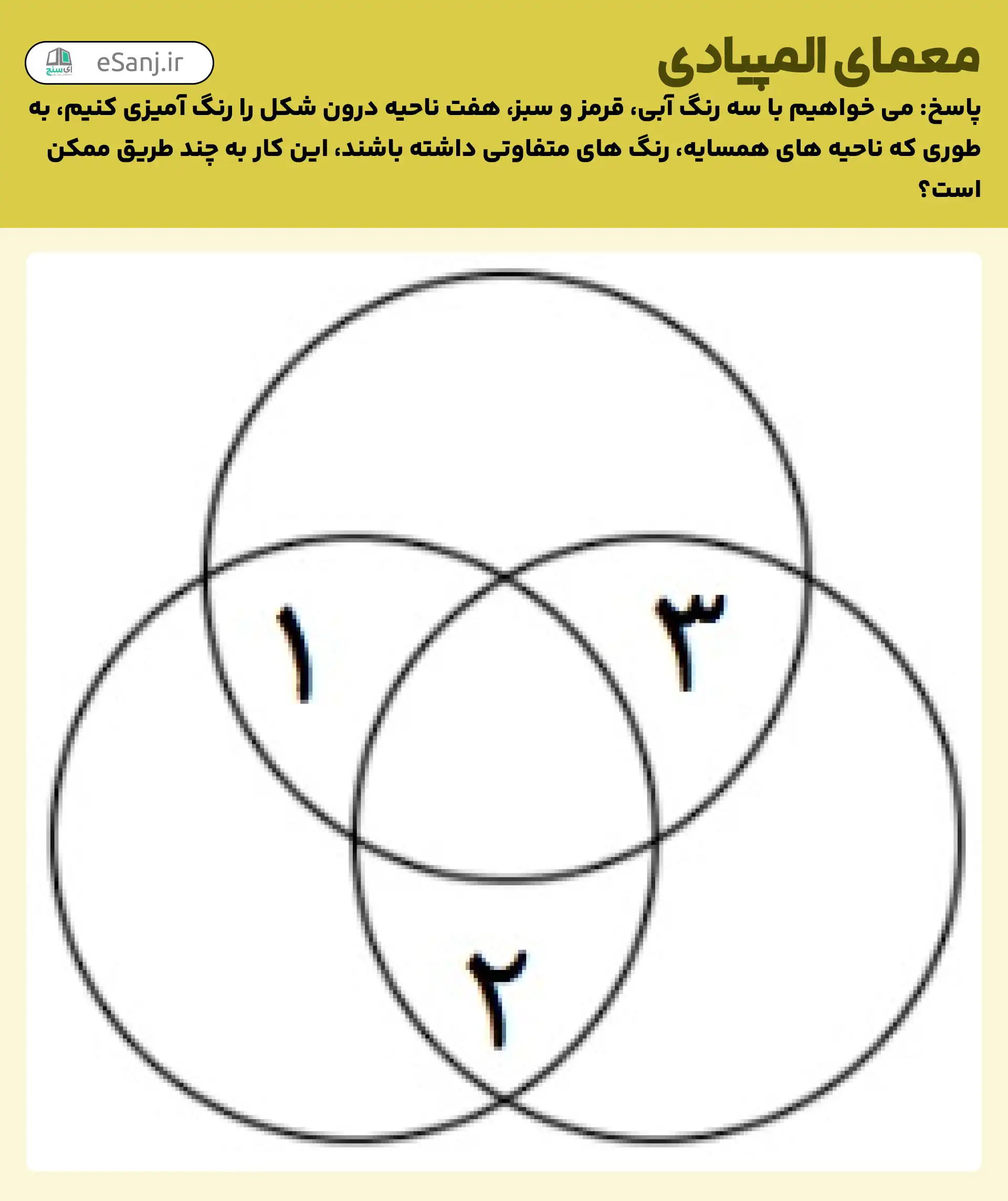
می خواهیم با سه رنگ آبی، قرمز و سبز، هفت قسمت درون شکل زیر را رنگ آمیزی کنیم، به طوری که ناحیه های مجاور، رنگ های متفاوتی داشته باشند؛ این کار به چند طریق ممکن است؟

به 84 طریق ممکن است.
فرض کنیم ناحیه های مشخص شده با اعداد 1،2،3 در شکل فوق به ترتیب دارای رنگ های x،y،z باشند. توجه کنید که تمامی رنگ های x، y، z نمی توانند متمایز باشند زیرا در غیر این صورت ناحیه مرکزی را با هیچ رنگی نمیتوان رنگ کرد. اکنون دو حالت را بررسی می کنیم:
حالت اول: x،y،z همرنگ باشند. در این حالت رنگ مشترک را می توان به 3 حالت انتخاب کرد. همچنین هر یک از دیگر نواحی را می توان به دو صورت رنگ آمیزی کرد. پس در این حالت، تعداد رنگ آمیزی ها برابر 48 خواهد بود: 3x2x2x2x2=48
حالت دوم: در میان x،y،z از یک رنگ دوبار و از یک رنگ یک بار استفاده شده باشد. برای انتخاب ناحیه ی با رنگ متمایز 3، برای انتخاب رنگ این ناحیه، 3 و برای انتخاب رنگ دیگر، 2 انتخاب داریم. پس برای مشخص نمودن رنگ ناحیه ی 1،2،3 در این حالت 3x3x2=18 روش متمایز داریم. حال توجه کنید که رنگ مرکزی به صورت یکتا، مشخص می شود چرا که از دو رنگ متمایز، همسایه دارد.
همچنین دو تا از نواحی گوشه ای نیز با هر دو رنگ مجاور هستند و رنگ این نواحی نیز بصورت یکتا مشخص می گردد. تنها ناحیه نامشخص ناحیه گوشه ای است که با دو ناحیه همرنگ مجاور است و در نتیجه می توان آن را به دو شیوه رنگ آمیزی کرد. پس در این حالت، طبق اصل ضرب، تعداد شیوه های رنگ آمیزی برابر 18x2=36 است.
پس طبق اصل جمع، تعداد راه های رنگ آمیزی شکل برابر 84=36+48 است.
معمای المپیادی شماره 11
یك جدول 9×9 از مربع های سفید داریم؛ حداكثر مقدار n را بر اساس آنچه می خواهیم، پیدا کنید:
اگر به هر طریق ممكن n تا از خانه های جدول را سیاه كنیم، باز هم در این جدول به توان چهار خانه ی سفید متوالی عمودی یا افقی پیدا کرد.

هر جدول ۴×۴ به وضوح حداقل ۴ خانه ی سياه نياز دارد تا هيچ ۴ خانه ی متوالی سفيدی در آن يافت نشود .
شکل سمت چپ در بالا يک مثال برای ۴ خانه ی سياه است. همچنين هر سطر يا ستون ۹ تايی برای اين که ۴ خانه ی متوالی سفيد در آن يافت نشود، حداقل ۲ خانه ی سياه نياز دارد و چون جدول ۹×۹ را میتوان به ۴ جدول ۴×۴ و دو رديف ۹ تايی مانند شکل ارنگ کرد.
پس حداقل ۲۰=۲×۲+۴×۴ خانه ی سياه نياز است تا هيچ ۴ خانه ی سفيد متوالی يافت نشود.
بر اساس شکل زیر:
۲۰ خانه ی سياه برای رسيدن به آنچه گفته شد، کفایت می کند. بنابراين با حداکثر ۱۹ خانه ی سياه نمی توان اين کار را کرد و حتماً ۴ خانه ی متوالی سفيد يافت خواهد شد.

معمای المپیادی شماره 12
با توجه به منطق شکل، خانه خالی را چگونه باید ترسیم کنیم؟
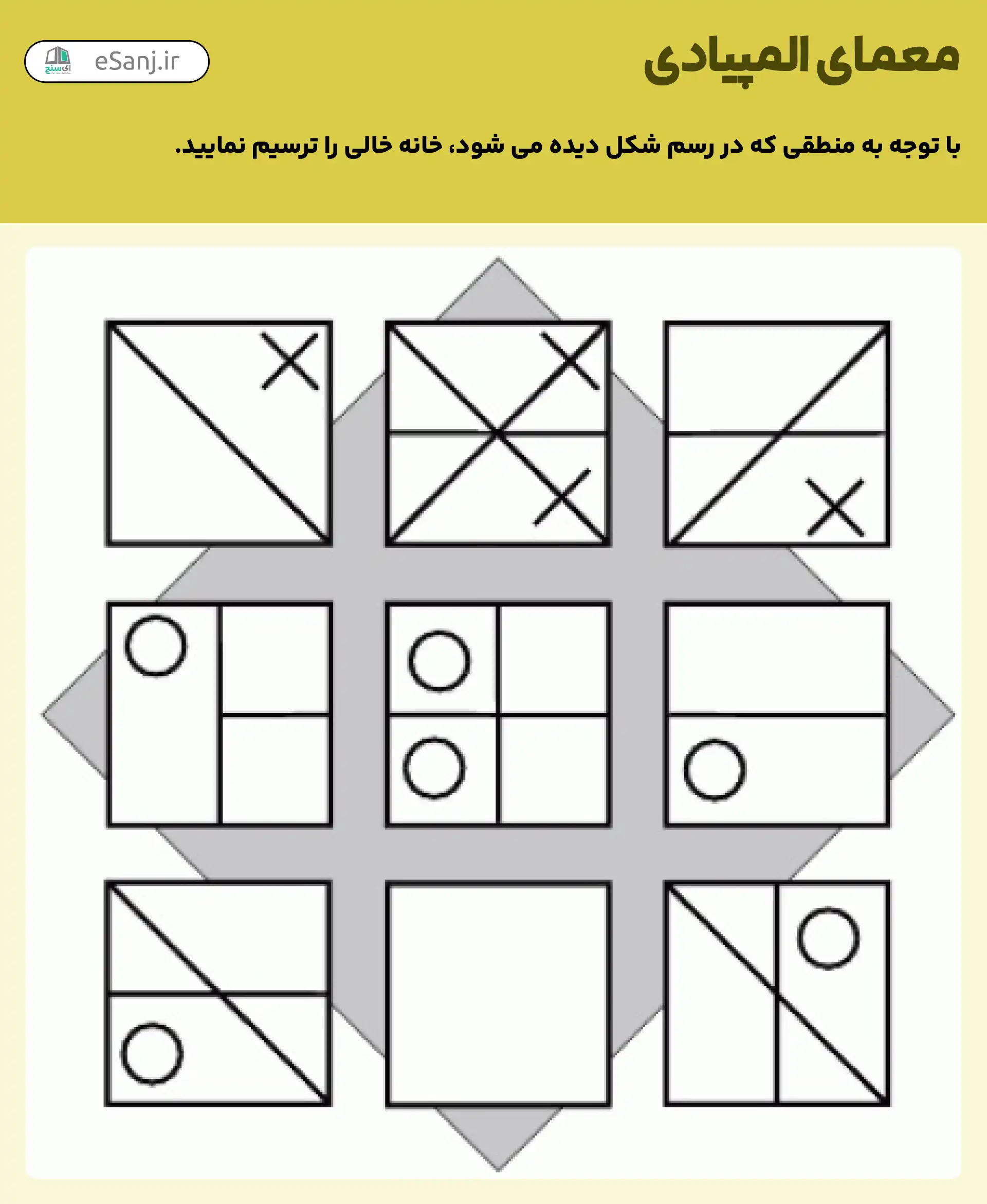
شکل باید بدین صورت باشد:

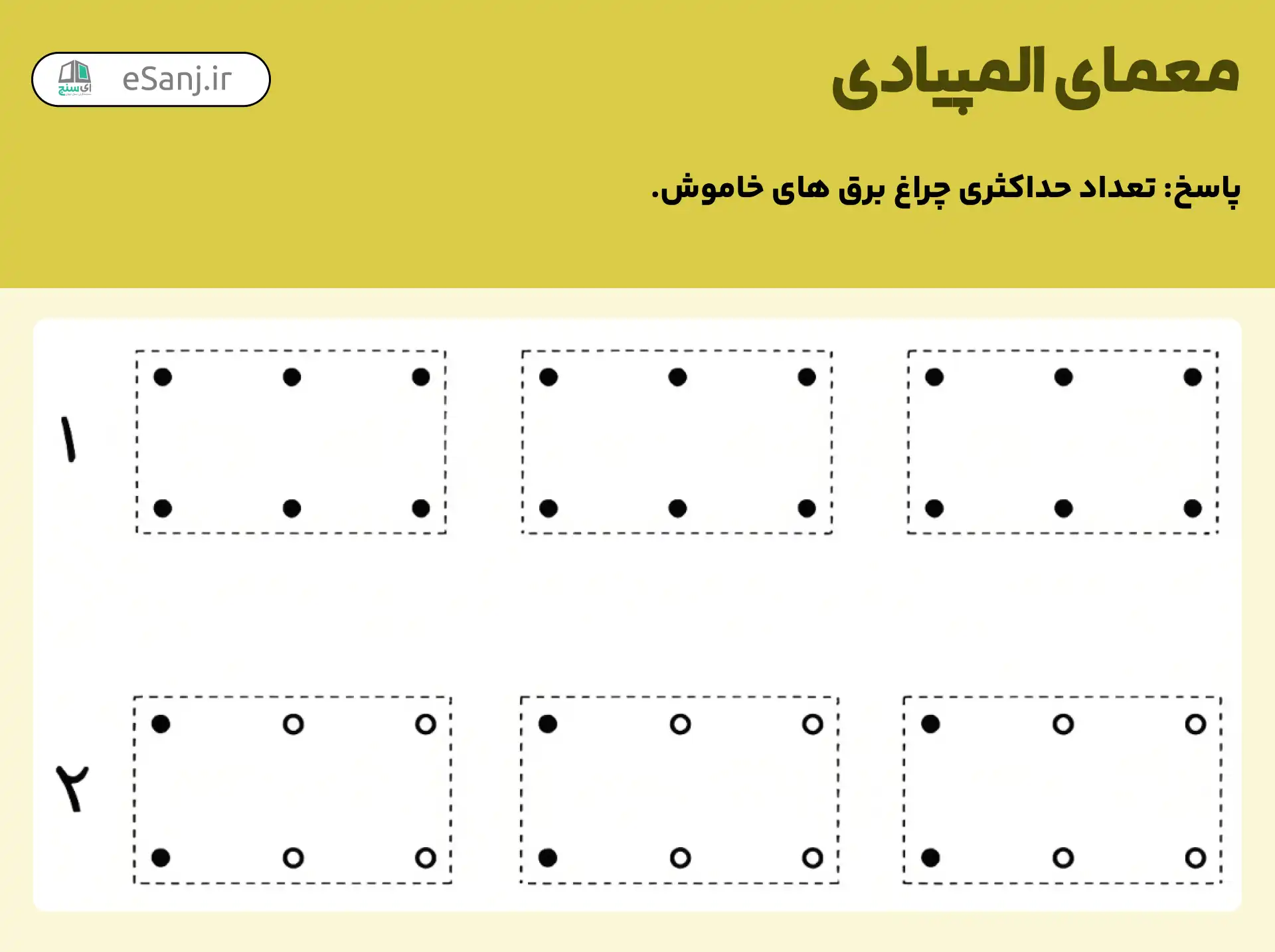
خیابان اصلی شهر را در نظر بگیرید؛ در این خیابان در دو ردیف 9 تایی، 18 چراغ برق در مقابل یکدیگر نصب شده اند که فاصله میان هر دو چراغ پشت هم، 50 متر و عرض خیابان 10 متر می باشد.
برخی از این چراغ ها خاموش هستند اما در فاصله کمتر از 60 متر، از هر چراغ خاموش حداکثر 3 چراغ خاموش دیگر وجود دارد.
به نظر شما چند چراغ خاموش است؟
بر اساس شکل زیر باید چراغ ها را به 3 دسته تقسیم کنیم: اگر در يک دسته بيشتر از ۴ چراغ خاموش باشد، پس يکی از دو چراغ وسطی آن دسته خاموش است. توجه کنيد از آن جا که اين چراغ از پنج چراغ ديگرِ هم ردیف خودش فاصله های کمتر از ۶۰ متر دارد، با اين فرض که در همسايگیِ ۶۰متریِ هر چراغ خاموش حداکثر سه چراغ خاموش ديگر قرار دارد تناقض دارد. پس در هر دسته حداکثر چهار چراغ خاموش داريم و بنابراين در کل حداکثر ۱۲ چراغ می تواند خاموش باشد.
شکل یک را در نظر بگیرید؛ این شکل از قسمت بالا تا پایین آن با اعداد 1 تا 8 شماره گذاری شده است؛ هر دو مکعب پشت هم به یکدیگر وصل بوده و فقط قابلیت چرخش نسبت به یکدیگر را دارند.
می خواهیم این شکل را به چند حالت مختلف داخل یک جعبه مکعب شکل به ضلع 2 جا دهیم؛
نکته: دو حالت مختلف برای شکل در نظر گرفته شده است؛ اگر دو قطعه با شماره های مختلف از بدن مار در یک مکان از جعبه ی مکعبی قرار بگیرند. یعنی اگر دو حالت با چرخش جعبه ی مکعبی به هم تبدیل شوند، یکسان نیستند.
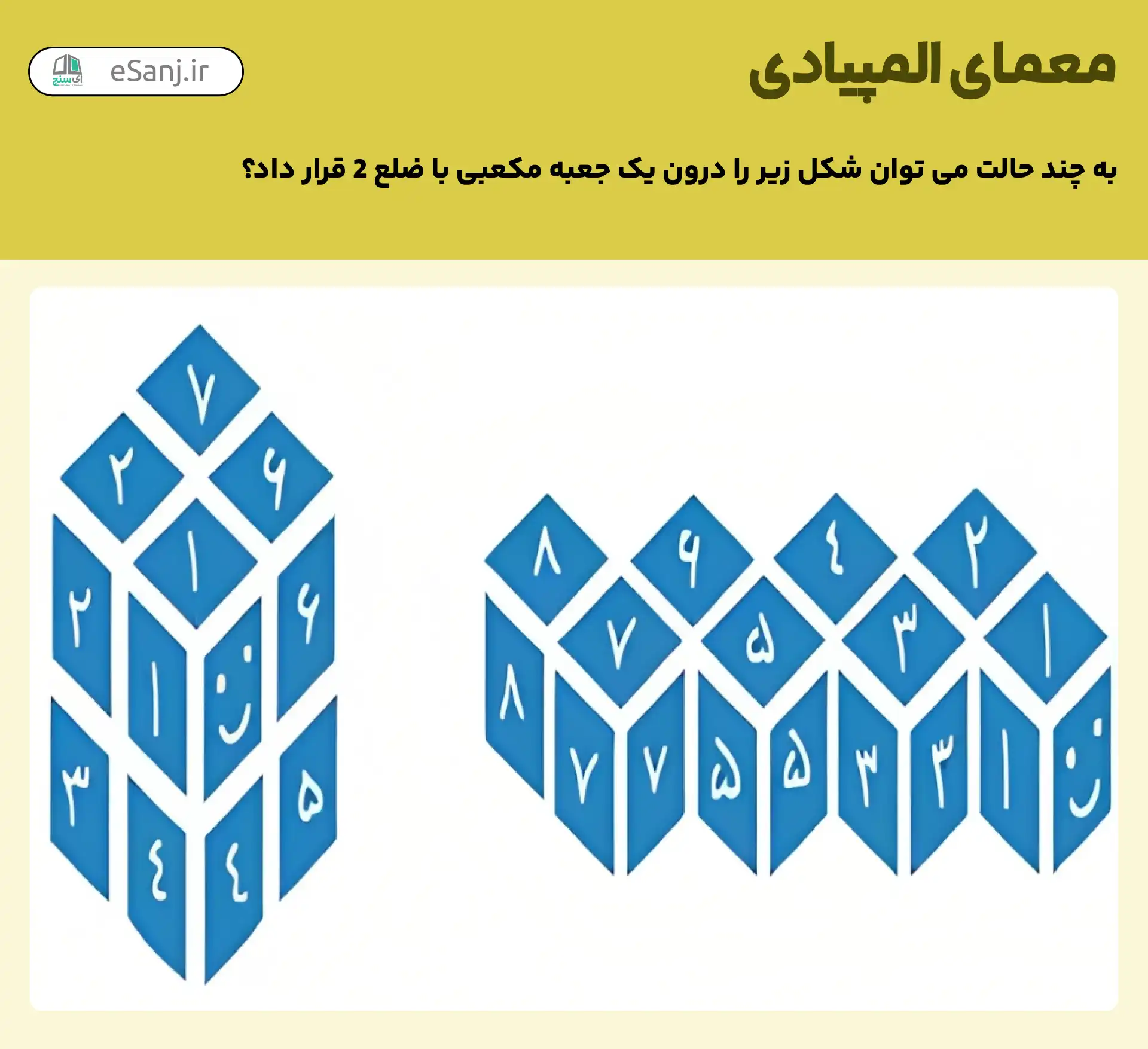
انتخاب سر مار 8 حالت دارد.
انتخاب دومی مستقل از اولی 3 حالت دارد و انتخاب سومی 2 حالت.
اما بعد از سومی حالت ها دیگر تقارن ندارند و نمی توان به این صورت شمرد. اما در کل بعد از انتخاب 3 تای اول، 3 حالت ممکن است پیش بیاید.
پس جواب برابر است با: 144=3×2×3×8
فقط 20 ثانیه فرصت دارید تا شماره پارکینگی که خودرو در آن پارک شده است را پیدا کنید!
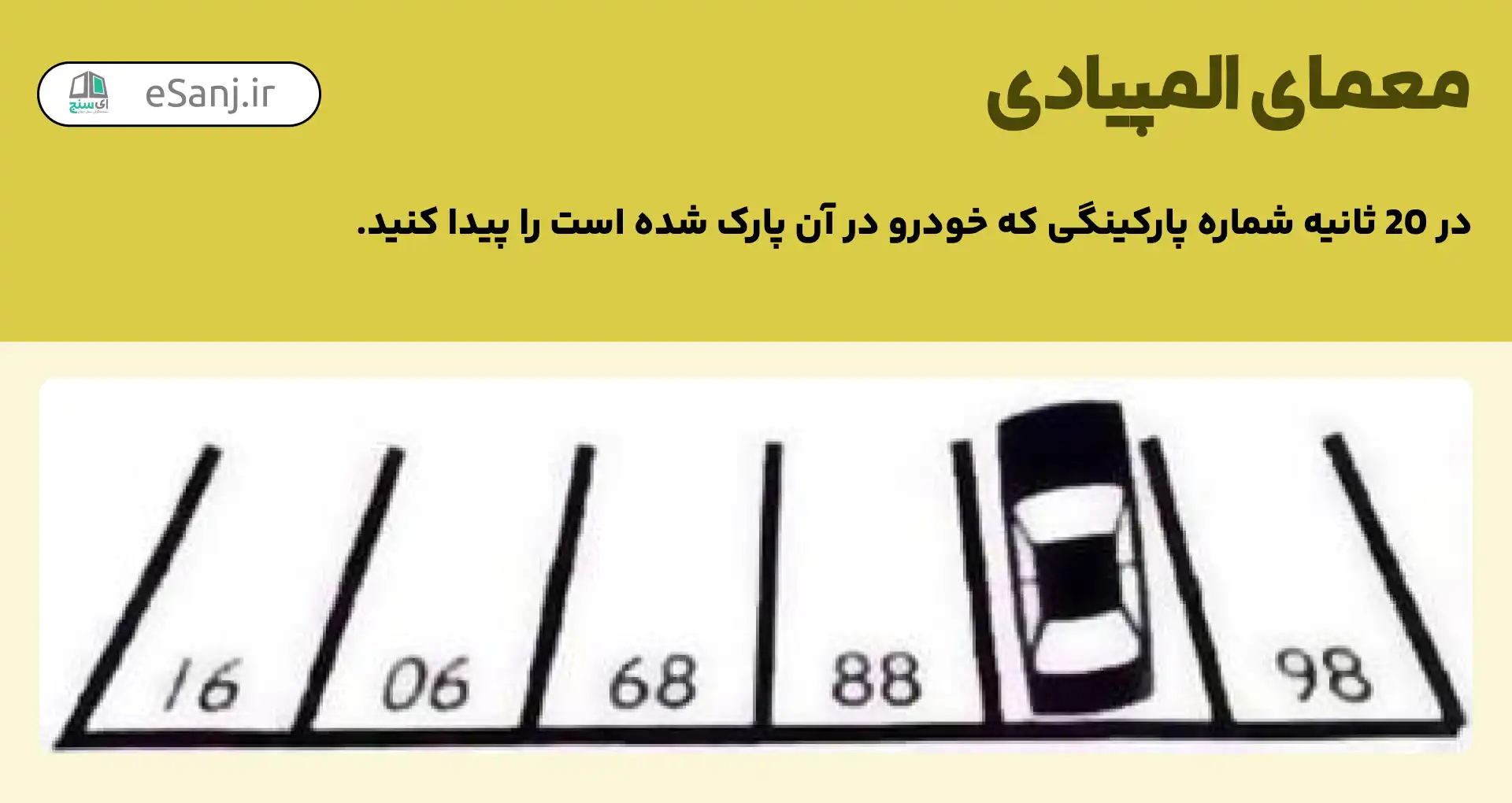
اگر اعداد را برعکس کنیم از ۸۶ شروع می شود و به سمت عدد ۹۱ می رود و جواب ۸۷ می شود.
یک شرکت راه سازی قرار است یک جاده 100 کیلومتری احداث کند؛ او برای ساخت این جاده برنامه زیر را ارائه داده است:
ماه اول: یک کیلومتر از جاده آماده است.
پس از ماه اول، هر ماه a10/1 کیلومتر از جاده آماده می شود. ( منظور از a، اندازه ساخته شده جاده تا ابتدای آن ماه است.)
بر اساس آنچه گفته شد، فکر می کنید جاده و آماده بهره برداری می شود؟
بعد از یک ماه، بخشی از جاده که آماده نشده است، از 100 کیلومتر کمتر است. بنابراین هر ماه دست کم 1/10010 کیلومتر از جاده ساخته می شود و به این ترتیب بعد از 10011 ماه، جاده آماده بهره برداری می شود!
چهار مادر به همراه فرزندان خود در یک مهمانی خانوادگی حضور دارند؛ کودکان شرکتکننده در این جشن، ۱، ۲، ۳ و ۴ ساله هستند. این مراسم، جشن تولد فرزند یلدا بوده است. رضا، بزرگترین کودک شرکت کننده در این جشن نبود. الهه یک سال پیش صاحب دختری به نام مهناز ش. در مهمانی بعدی که جشن تولد است، فرزند باران، سومین جشن تولد او خواهد بود. یکتا بزرگتر از دانیال است. فرزند یگانه، بزرگ ترین کودک این مراسم و دانیال از فرزند باران بزرگتر است.
با توجه اطلاعات بالا نام مادر، فرزند و سن فرزندان را مشخص کنید.
نام مادر: الهه/ نام فرزند: مهناز/ سن فرزند: یک ساله
نام مادر: باران/ نام فرزند: رضا/ سن فرزند: دو ساله
نام مادر: یلدا/ نام فرزند: دانیال/ سن فرزند: سه ساله
نام مادر: یگانه/ نام فرزند: یکتا / سن فرزند: چهار ساله
سه خواهر می خواهند مبلغ 36 میلیون تومان را میان خود تقسیم کنند؛ به هر کدام از این خواهر ها بر حسب سنی که دارند پول رسیده است.
خواهر کوچکتر نصف پول خود را به صورت مساوی میان دو خواهر دیگر تقسیم می کند و خواهر وسطی و بعد خواهر بزرگ تر هم همین کار را انجام می دهند، در نهایت پول هر سه خواهر مساوی می شود. به نظر شما خواهر وسطی چند ساله است؟
او ده سال و نیم سن دارد؛ در نهایت پول هر سه خواهر باهم برابر شده است پس در پایان مرحلهی سوم هر کدام از آنان 36/3 یعنی ۱۲ میلیون تومان خواهند داشت. قبل از این مرحله (پایان مرحله دوم) خواهر بزرگ تر یقینا ۲ میلیون تومان داشته است (چون نصف پولش را برای خودش نگه داشته و نصف پولش را بین دو خواهرش تقسیم کرده است.) چون خواهر بزرگ تر نصف پولش را بین دو خواهر دیگر به صورت مساوی تقسیم کرده است پس به هرکدام از آنان ۶ میلیون تومان داده است.
پس قبل از شروع مرحلهی پایانی پول خواهر بزرگ تر ۲۴ میلیون تومان، پول خواهر وسطی۶ میلیون تومان و پول خواهر کوچک تر ۶ میلیون تومان بوده است.
با همین استدلال در ابتدای مرحلهی دوم خواهر بزرگ تر ۲۱ میلیون تومان، خواهر وسطی ۱۲ میلیون تومان و خواهر کوچک تر ۳ میلیون تومان دارند و بالاخره در ابتدای مرحلهی اول خواهر بزرگ تر نوزده و نیم میلیون تومان، خواهر وسط ده و نیم میلیون تومان و خواهر کوچک تر شش میلیون تومان پول دارند.
یک سالن با ۱۰۳ ردیف صندلی داریم که در هر ۵ ردیف متوالی آن در مجموع ۲۰۰ نفر نشستهاند. در این سالن حداقل و حداکثر چند نفر نشستهاند؟
حداکثر تعداد نفرات زمانی است که در هر یک از ردیفهای ۱۶،۱۱،۶،۱،…،۹۶ و ۱۰۱ دقیقا ۲۰۰ نفر و در هر یک از سایر ردیفها۰ نفر نشسته باشند که در این حالت تعداد نفرات 21×200 یعنی ۴۲۰۰ خواهد شد.
حداقل تعداد نفرات نیز زمانی است که در هر یک از ردیفهای ۱۵،۱۰،۵،… و ۱۰۰ دقیقا ۲۰۰ نفر و در هر یک از سایر ردیفها ۰ نفر نشسته باشند که دراین حالت تعداد نفرات 20×200 یعنی ۴۰۰۰ خواهد شد.
معلم برای انجام یک کار گروهی می خواهد، ۶ دانشآموز را گروه بندی کند؛ به طوری که هر گروه یا تک نفره یا شامل ۲ دانشآموز باشد. به چند طریق این کار ممکن است؟
76 طریق.
اصطلاحات مهم این مقاله
سوالات متداول
-
آیا حل معمای المپیادی سخت است؟
- بله حل کردن اینگونه معماها نیاز به تفکر و تامل دارد.
-
چه کسانی می توانند معماهای المپیادی حل کنند؟
- سطح اینگونه معماها سخت و دشوار است، بنابراین برای حل اینگونه معماها به دانش ریاضی و توانایی حل مسئله نیاز است.
-
برای حل معماهای المپیادی به چه چیزهایی نیاز داریم؟
- توانایی حل مسئله، تامل، تفکر، توانایی استدلال، توجه و تمرکز و....